Viral Symmetry and Genetic Economy
Throughout history viruses have consistently emerged as important pathogens with distinct genetic organizations, replication strategies, and biophysical properties. However, despite this incredible diversity in virus organization, nearly all known virus structures subscribe to the rules of geometric symmetry. It’s a matter of (genetic) economics!
In Building Viruses, Symmetry is (Almost) Always Key
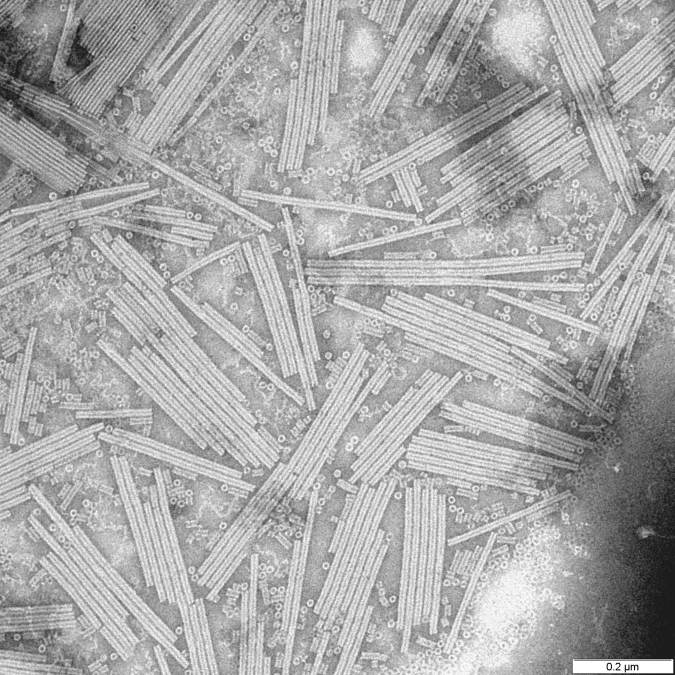
Electron micrograph of Tobacco Mosaic Virus (TMV), a helical RNA virus studied by Franklin, Watson, and Crick.
While Rosalind Franklin and her colleagues, James Watson and Francis Crick, might be best known for their contributions toward our understanding of DNA structure, they, along with a few other colleagues, spent a lot of time thinking about viruses. These scientists noted that viruses typically came in one of two shapes: rods or spheres. Additionally, they maintained that each virus shape maintained a specific symmetry. But why?
Alluding to the concept that scientists would later term “genetic economy,” Watson and Crick concluded in their 1956 Nature report:
[A virus] shell is necessarily rather large, and the virus, when in the cell, finds it easier to control the production of a large number of identical small protein molecules rather than that of one or two very large molecules to act as its shell. These small protein molecules then aggregate around the ribonucleic acid in a regular manner, which they can only do in a limited number of ways if they are to use the same packing arrangement repeatedly. Hence small viruses are either rods or spheres.
In other words, the size of a virus is much bigger than we expected given their relatively small genomes. The viral genome provides the instructions for a small number of capsid subunits, the viral packaging protein(s), that are subsequently made (by host cell machinery) in large quantities. Watson and Crick thought that identical protein subunits interact with each other in a way that is the same throughout the capsid, with a maximal number of connections for each subunit. The result of this “genetic economy” is symmetry in capsid structure. Furthermore, Watson and Crick postulated that the interactions between subunits had to be non-covalent so that viruses could come apart when they infect a cell. This makes sense because in order to break a covalent bond, you need to add energy. Viruses are not metabolically active, and do not produce or consume energy (they do not make ATP!). As it turns out, the non-covalent nature of capsid protein interactions allow for reversible, error-free particle assembly.
Example of icosahedral symmetry in viruses, from Nat Commun 10, 4414 (2019)
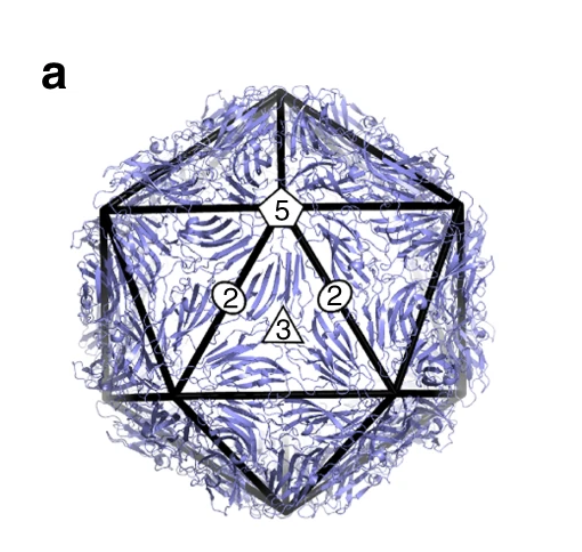
As Watson and Crick continued to examine the proteins that make up the capsid of spherical viruses, they noticed that the shapes of protein subunits were highly irregular. This inspired them to explore how a virus can be round given the irregular shapes of these capsid proteins. They leaned on two key clues. First, they noticed that all spherical capsids had exact numbers of proteins, and that this number would always be a multiple of 60. Secondly, they noticed that individual proteins that made up the capsid were relatively similar in size (each protein would fall between 20 – 60 KDa). This essentially meant that bigger capsids were NOT made of bigger proteins, but rather these larger structures consisted of more units of these proteins. Their suggestion was that spherical viruses adopted icosahedral symmetry (like a soccer ball), allowing them to build a complete, entirely closed capsid coat using the smallest possible number of subunits (genetic economy, FTW!). Long story short, efficiency is the name of the game when it comes to viral genetics, and the packaging proteins are no exception.
With experimental approaches centered on electron microscopy and x-ray diffraction, this hypothesis was later confirmed and expanded upon by scientific peers of Franklin, Watson, and Crick: Donald Caspar and Aaron Klug. Their experimental findings, shared with the scientific community in 1962, introduced the Caspar-Klug theory of viral symmetry for spherical viruses. This theory described capsids from spherical viruses as having icosahedral symmetry, but demonstrated that spherical viruses were not themselves “true” icosahedrons — meaning that they do not look like a polyhedron with 20 equilateral triangular faces (like the D20 die from Dungeons & Dragons).
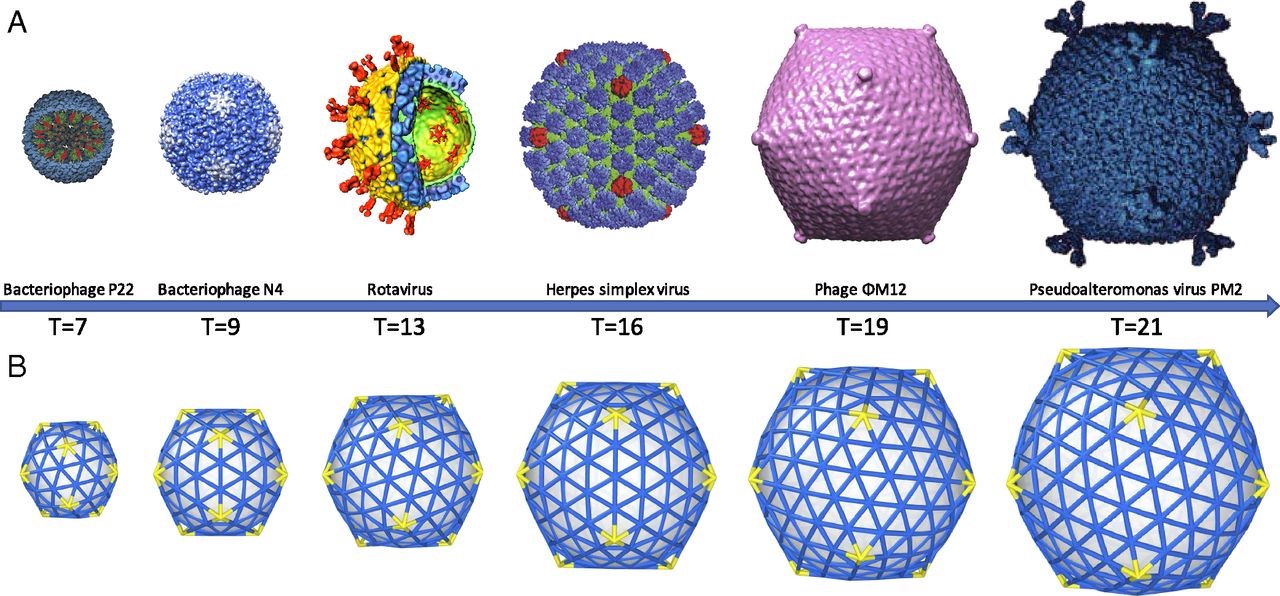
Examples of how spherical viruses maintain icosahedral symmetry. Image reprinted from , , , &
The Caspar-Klug theory was fairly consistent with what Watson and Crick had proposed a few years earlier, except that Caspar and Klug demonstrated that interactions among protein subunits were not exact, as Watson and Crick initially suggested. Instead, they demonstrated that the proteins making up each of the structural units of a viral capsid interacted in a way that was “quasi-equivalent” (similar, but not exactly the same). The quasi-equivalent characteristic allows protein subunits to configure themselves in a way that maintains icosahedral symmetry (and genetic economy) in a spherical capsid, regardless of capsid size.
Despite being created during the early echoes of the field of virology, the Caspar-Klug theory has held up incredibly well, with a few notable exceptions (i.e. the giant pandoravirus). You can play around with models of virus symmetry through an origami activity created by RCSB PDB. You can also see how Columbia University Professor, Vincent Racaniello, models helical and spherical virus symmetry using magnetic bucky balls in the video below.
Full versions of the Watson and Crick 1956 Nature report and the Caspar and Klug 1962 research article can be found in the ‘save and share’ section on this page.
References
Caspar, D. L., & Klug, A. (1962). Cold Spring Harb Symp Quant Biol, 27, 1-24. Physical principles in the construction of regular viruses.
Crick, F. H. C., & Watson, J. D. (1956). Structure of small viruses. Nature, 177, 473–475. https://doi.org/10.1038/177473a0
Li, S., Roy, P., , A., & Why large icosahedral viruses need scaffolding proteins. [Image].
Venkataram Prasad, B. V. & Schmid, M. F. (2012). Principles of virus structural organization. Adv Exp Med Biol, 2012, 726, 17–47. doi: 10.1007/978-1-4614-0980-9_3
Knipe, D. M., & Howley, P. M. (Eds.). (2013). Fields virology. Lippincott Williams & Wilkins.
Twarock, R., Luque, A. Structural puzzles in virology solved with an overarching icosahedral design principle. Nat Commun 10, 4414 (2019). https://doi.org/10.1038/s41467-019-12367-3
